TCD2017.mws6.html

Some classic congruences (Fermat, Wilson, Lagrange, and some others ... ), and the Gauss- Wilson theorem

Fermat's 'little' Theorem, and introducing a standard term: the Fermat quotient,

An exercise concerning 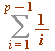, and the half and quarter sums 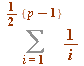and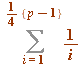

Wilson's Theorem, and introducing another standard term: the Wilson quotient,

Wilson's theorem went in two different directions, what one might call:

the Gauss (1777-1855) path (part of his monumental DISQUISITIONES ARITHMETICAE of 1801)

The Lagrange path

And now the Gauss path:

The Gauss-Wilson theorem