An exercise concerning 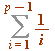, and the half and quarter sums 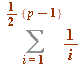and  

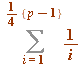
First, an exercise for you: prove, for an odd prime , that the numerator (of the fraction) in the sum: 

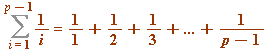
is (i.e., is divisible by ). 

_________________ 

But now, two less obvious sums, the first due to Eisenstein (early 1800s), the second to Lerch-Glaisher (~ 1900): 

• for any odd prime 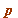, the ' half ' sum:

satisfies . 

>

L := []: for p from 3 to 50 do if isprime(p) then             q||p := (2^(p-1) - 1)/p: ### the Fermat quotient base 2             S||p := add(1/i, i = 1..(p-1)/2): ### the half sum                 L := [op(L), p]: fi od:      print(``); p := 'p': print(``); print(array([['p', ``, ``, 'S[half]', ``, q['p'](2), ``, S[half], ``, -2*q[p](2)], seq([p, ``, ``, S||p, ``, q||p, ``, S||p mod p, ``, -2*q||p mod p], p = L)])): print(``); lprint(`The last two columns are mod p reductions.`);

 

 

 

 

 

`The last two columns are mod p reductions.`

 

>

 

• for any prime 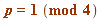, the ' quarter ' sum:

satisfies . 

>

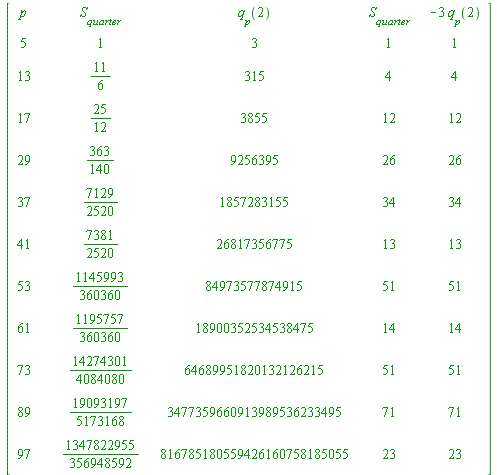
L := []: for p from 5 by 4 to 100 do if isprime(p) then             q||p := (2^(p-1) - 1)/p: ### the Fermat quotient base 2             S||p := add(1/i, i = 1..(p-1)/4): ### the QUARTER sum                 L := [op(L), p]: fi od:      print(``); p := 'p': print(``); print(array([['p', ``, ``, 'S[quarter]', ``, q['p'](2), ``, S[quarter], ``, -3*q[p](2)], seq([p, ``, ``, S||p, ``, q||p, ``, S||p mod p, ``, -3*q||p mod p], p = L)])): print(``); lprint(`The last two columns are mod p reductions.`);

 

 

 

 

 

`The last two columns are mod p reductions.`

 

>

 

Remark. This congruence holds for primes ; all that is required is instead of .