The Gauss-Wilson theorem 

Let us ask: is there a composite analogue of the earlier Wilson's theorem: 

(mod ) 

Meaning: is there anything of interest that may be said about the value (mod ) for composite values of ? 

There is of course a completely trivial analogue: 

>	L := []: for n from 2 to 40 do if isprime(n) = false then L := [op(L), n]: fi od: print(``); print(array([ ['n', ``, ``, '(n-1)!', ``, ``, 'residue'], seq([n, ``, ``, (n-1)!, ``, ``,(n-1)! mod n], n = L)])): print(``); lprint(`The final column show the LEAST ABSOLUTE residue of (n-1)! mod n.`);

 

 

 

 

`The final column show the LEAST ABSOLUTE residue of (n-1)! mod n.`

 

>

 

and I leave it to you to establish this elementary result: 

• if 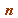is composite then - with the sole exception of 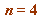- then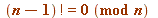

Of course it is easy to see why this triviality is occurring. 

This, now, is what Gauss did (and included in his monumental DISQUISITIONES ARITHMETICAE of 1801):

DEFINE (our notation, and our notation and terminology, not Gauss', who didn't make a notation nor term for this: 

(the 'Gauss factorial of with respect to ') 

to be the product of all residues in the interval [] that are relatively prime (the standard terminology) to .  

'relatively prime to ' means simply that they do not share a common prime factor. 

Example. If we choose then the Gauss factorial of with respect to  

would be the product of all those whole numbers between 1 and 44 that are not divisible by a 3 or a 5: 

So, let's start with all the integers between 1 and 44: 

>	print(``); L44 := [seq(k, k = 1..44)];

 

 

	(5.5.1)

 

>	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44]

 

First I highlight all those divisible by 3: 

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,

16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30,

31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 

Now I remove those, and of those which remain I further highlight those divisible by 5: 

1, 2, 4, 5, 7, 8, 10, 11, 13, 14,

16, 17, 19, 20, 22, 23, 25, 26, 28, 29,

31, 32, 34, 35, 37, 38, 40, 41, 43, 44 

and then remove those, leaving, in the process, precisely those residues between 1 and 44 that are 'relatively prime' to 45: 

1, 2, 4, 7, 8, 11, 13, 14,

16, 17, 19, 20, 22, 23, 26, 28, 29,

31, 32, 34, 37, 38, 41, 43, 44 

Here they are in a list: 

>	n := 45: LL||(n-1) := []: for k to (n-1) do if igcd(n, k) = 1 then LL||(n-1) := [op(LL||(n-1)), k]: fi od: print(``); LL||(n-1);

 

 

	(5.5.2)

 

>	nops(LL||(n-1));

 

(5.5.3)

 

The product, then, of those (24, as it happens) residues is the Gauss factorial of with respect to  

That '24' is known as the 'Euler phi-value of 45' (notation ). 

Note. There is a beautiful formula - due to Euler - for : let be factored into its (unique, a fundamental theorem) prime decomposition 

distinct primes and positive powers , then 

>

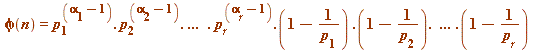
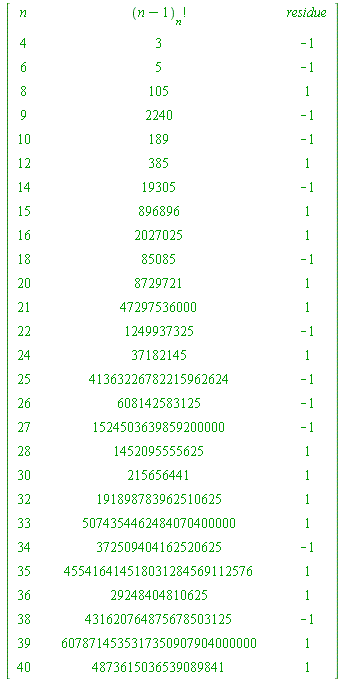
L := []: for n from 2 to 40 do if isprime(n) = false then                  r := 1:    for k from 2 to (n-1) do if igcd(n, k) = 1 then r := r*k fi od:               R||n := r: L := [op(L), n]: fi od: print(``); print(array([ ['n', ``, ``, '(n-1)[n]!', ``, ``, 'residue'], seq([n, ``, ``, R||n, ``, ``,PI(n, 1, 1)], n = L)])): print(``); lprint(`The final column show the LEAST ABSOLUTE residue of GAUSS FACTORIAL (n-1)[n]! mod n.`);

 

 

 

 

`The final column show the LEAST ABSOLUTE residue of GAUSS FACTORIAL (n-1)[n]! mod n.`

 

>

 

The Gauss-Wilson Theorem (discoverable by anyone) is this: 

For any integer (prime or composite) we have: 

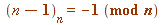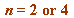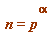• if and only if or   or 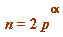, for an odd prime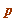
  

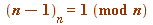• otherwise (of course for 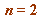as well)

Aside. Only for do we have both 1 and 2 holding.