later developments
Home Up

 

 

New Composite Fermat Number Records
in February and October 2003 

On Monday 17th February 2003, Thomas Walsh (one of my college Proth-Gallot Group) - [1] here is Thomas eight days later, with Jacqueline Fallon, another member of my computation group, and here [2] Thomas points at his results file - found a George Woltman PRP-discovered 645817-digit probable prime p = (3X22145353 + 1) [3] on his computer (I had already done sieve work with Paul Jobling's NewPGen). 
   

    That evening, at home, I began using Yves Gallot's Proth program to check for the (almost certain) primality; that would normally entail two independent Proth tests, followed by the tense period of Fermat and generalised Fermat number testing. By Wednesday 19th (after 40 hours, the first round was over: [4] a definite prime), but later that day Yves sent me a modified program which would allow me to split the nerve-jangling sequence of calculations: some at home and some here in my office. 
   

At exactly 14:56:24, at home, on Friday 21st I saw (in a heart-stopping moment; actually for several seconds I couldn't bring myself to look...) that (3X22145353 + 1) [5] divided the 2145351th Fermat number, breaking the previous record set in July 1999 by Yves Gallot and me. (I don't have a digital camera, so I transferred my home Proth screen to college, by saving the .dta etc files to a floppy, and temporarily reran a second version of Proth here at my desk).
   
Shortly afterwards I sent off an official notification to the Number Theory Mailing List. Wilfrid Keller's outstanding Fermat number site (which will inform you of who did what, and when, right back to Euler's finding of a factor of the fifth Fermat number in 1732) is here, and there is simply nowhere better to look for information on primes in general than Chris Caldwell's leading prime number site.

     Wilfrid Keller (WK) and Chris Caldwell (CC) maintain current details concerning generalised Fermat numbers for the 'historic' bases (6, 10 and 12):  WK6, WK10, WK12, CC6, CC10, CC12. Now (March) I have reported that the above prime attains a new record for all the historic bases: 3, 5, 6, 10 and 12. These three photos show the final Proth-Fermat screens for all the new records: [6] two screens, [7] Proth prime and GFNs, and [8] GFNs. 

     My thanks to Paul Murphy for all the above digital photos.

     Ivars Peterson devoted his Science News MathTrek article of 1st March 2003 to the above discovery.


On Tuesday 7th October 2003 I noticed the 746190-digit probable prime 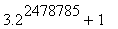on the computer of M�ire N� Bhaoill (M�ire is one of my St Patrick's College computational group). I had done, as always, the preliminary sieve work with Paul Jobling's newpgen program, and the probabilistic primality testing with George Woltman's PRP program. By Friday 10th (3X22478785 + 1) had been established to be a deterministic prime (using Yves Gallot's Proth program), and to be a factor of the 2478782nd Fermat number (screen photo), using Yves Gallot's GFN program. I sent notification within hours to the Number Theory Mailing List. The size of that Fermat number almost defies belief: to write it out in decimal notation (i.e. in the normal fashion), at, say 4 digits per inch in the horizontal and vertical, would require a square whose side exceeded 10373075 LIGHT YEARS... (interested readers may read my elementary analysis of that topic in the 1999 Fermat Record Number corner of this site). The above October discovery breaks the previous record announced in February 2003.

�