A very brief introduction

I suppose everyone knows that is irrational, and has read the standard textbook proof, with its we may suppose without loss of generality that is in reduced form... . I hate the standard textbook presentation of the proof. I don't hate the proof ; rather I hate the presentation .

Sadly (in my view) youngsters don't get a chance to think before being exposed to its brutal irrationality proof that rambles on about "we may suppose that ... may be expressed in reduced form" (even G. H. Hardy - an early hero of mine - is guilty of it in his classic A Mathematician's Apology ). Youngsters should be given an opportunity to attempt to find a 'fraction' - a term that youngsters probably prefer over 'rational number' - that possibly equals (of course they're in for a surprise). Since that is a topic on which I have already written at considerable length in my 56-page Number theorising with Talented Youth (available from the Talented Youth corner of my web site) then I will not pursue it here.

Briefly, how do I think irrationality (as a subject to be contemplated) can/should be introduced to youngsters? From my experience, many youngsters think that is 1.414... (the calculator displayed value):

> evalf(sqrt(2), 10);

>

A thoughtful student - when pressed - will tell you that 1.414213562 is not because, when you square it, you get a decimal that ends in a 4, and so it can't be 2. More pressing (that could be motivated by by further computations like:)

> evalf(sqrt(2), 40); # this "really ends" in '7'

>

will lead - with proof (the crux!) - to the conclusion that does not have a terminating decimal value. That's an elementary, but serious result. (Aside. What, though, is the non-terminating decimal value of ; what are its digits? Once, when I was a student in London, I sat with a group of other students in the company of C. A. Rogers. Someone asked him which question he would most like to have answered. He replied: to know the decimal expansion of the square-root of two . We all knew what he meant. Many years later, in June 1986, I travelled to London to attend the UCL meeting marking C.A.R.'s retirement. Looking back over his life, Rogers remarked on his good fortune to have had a good teacher at school, and he mentioned the friendly competition that he had later enjoyed with Wolfgang Schmidt.)

Next, in my view (based on teaching experience ) the discussion can continue on this line of observation (followed by appropriate questioning): numbers with terminating decimal values are simply fractions with a very particular type of denominator (powers of 10), and so saying (e.g) that is not 1.414 is simply saying that it is not 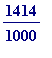, but (the motivated question) could it be (say) ? Well, let's see:

> evalf(1414/999);

>

So, it isn't. But could it be something else ? Some other fraction? Could it be (say) ?:

> evalf(sqrt(2), 10);
evalf(47321/33461, 10);

No. And why not? Resorting to computation we see they aren't equal, as they differ on the last decimal point:

> evalf(sqrt(2), 11);
evalf(47321/33461, 11);

But could be (say) ?:

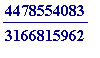> evalf(sqrt(2), 20);
evalf(4478554083/3166815962, 20);

>

Again, no. But why not? And this is the point at which one can start asking for reasons independent of computation. Of course it's also the time to start asking: where are those fantastic fractions coming from? It's the sort of thing - if you don't know about this - you may read about in the Talented Youth corner of my web site, or in my ICTMT4 Plymouth 1999 talk on L- and R-approximations , or in the first year section of my Courses I Teach corner of my web site.

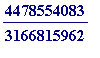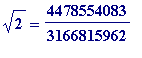Why can't be ? Suppose it was, then , and then?

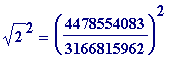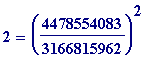, , and?

2* 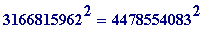(and then what?)

Impossible since... (e.g.: the LHS ends in '8', the RHS ends in '9'; the LHS is even, the RHS is odd). That's not the end of it, of course. But it all eventually leads to having a proof that is irrational . In short, by following a well-motivated path, one may lead young minds to a basic understanding of the fundamental mathematical concept of irrationality. If we are interested in teaching, then this - or something like it - is what we should be doing. Incidentally, a much faster route into irrationality may be given by asking questions like:

• Is (as the old log tables used to show)?
• Is (as ones calculator may show, or, in Maple)?

> evalf(log[10](2));

>

Then, having easily argued that does not have a terminating decimal value, move on to easily argue that it is, in fact, irrational. While numbers like (e.g.) and are both irrational - the latter having the easier irrationality proof - these two numbers are fundamentally quite different : the former is an algebraic number, while the latter is a transcendental number. But I am getting ahead of myself. It is time I moved on to the next section.