Carl Ludwig Siegel (1896-1981)

I mention only a small fraction of Siegel's achievement, and in the process am omiting many remarkable results.

Siegel's (1917) Theorem . Let be any real algebraic number of degree n ( at least 3), and let be any positive constant ( however small ), then there is a positive constant (i.e. the value of c depends

only on and ) such that

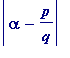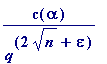> ... (i'')

and Siegel conjectured that the above inequality could be improved to

>

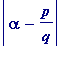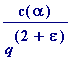
which, if true, would, of course, be best possible (in a sense), since by a classic (and easy to prove theorem of Dirichlet) one has: for every real irrational number there are infinitely many distinct rational numbers ( p and q integers, with ) such that

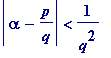
Siegel was the first to prove transcendence results involving elliptic functions.

Siegel's (1932) Theorem . Let P( z ) be the Weirstrass elliptic function with algebraic number invariants and in the equation (the standard connection between P( z ) and its derivative P '( z )), then at least one of any fundamental pair of periods of P( z ) is transcendental.

At the end of chapter 3 of his book Transcendental Numbers , the one dealing with Hilbert's seventh problem, Siegel wrote (to illustrate the state of ignorance, I have slightly changed Siegel's notation and wording, and made some emphases): The result on the transcendency of can also be stated this way: If are algebraic numbers, , , then the ratio is either rational or transcendental. In other words, the logarithm of any algebraic number relative to any algebraic base is either rational or transcendental. However...it is not even known whether there cannot exist an inhomogeneous linear relation with quadratic irrational .

And that question of Siegel's concerned only two logarithms, with severely restricted (though completely non-trivial) quadratic algebraic . What a later triumph it was for Alan Baker to completely settle, not just that question of Siegel, but the completely general version of it: n logarithms, and algebraic s. I will come to that in the later Baker section.

At the end of that same chapter Siegel also remarks: Another example showing the narrow limits of our knowledge on transcendental numbers is the following one: Since e and are both transcendental, not both numbers and can be algebraic [that, by the way, is simply a particular case of a completely general remark, namely: if are both transcendental, then and cannot both be algebraic] ; but we do not even know whether or are irrational.