Fast track observations & questions after Liouville

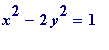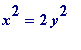Observation. In connection with the irrationality of (e.g.) one comes to know that the important result that the equation has an infinite number of solutions in (positive) integers x , y . One may think of that as starting from the meaning of 's irrationality: there are no (positive) integers x, y such that , and so the next best thing is to have 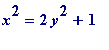(or 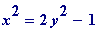) (An interested reader, not familiar with this, would benefit, I believe, from reading my web site notes on - what I call - L- and R-approximations. 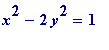In general it's not just that would be of interest, but , and thus not just , but ).

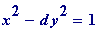Every such x , y leads to a fantastic rational approximation to , as good an approximation, in fact, as there can possibly be. Slightly throwing away some of the quality of approximation, one has:

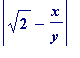< (infinitely often, in fact) (i)

Now, inequality (i) happens to be (independently) gauranteed by the completely general:

Theorem (Dirichlet). Let be any real irrational number (and it doesn't matter whether is algebraic or transcendental), then there are an infinite number of rational numbers ( p , q integers, q > 0) such that

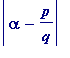< ... (ii)

Question. Are there any such s for which a better approximation than (ii) could happen?

Answer. Yes, of course. It's easy. By simply varying the type of number encountered in the Liouville section, and forming a number like (e.g.) 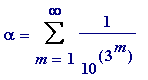then one obtains an for which the inequality

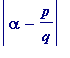< ... (iii)

has an infinite number of solutions in rational numbers (a careful reader will immediately spot that I haven't quite got the full validity of (iii), but almost , and it requires nothing more than than gorey extra detail to get the full validity...)

Another question. And how many such s can one get?

Immediate answer, and observation. It's easy, and again - like I've already pointed out in the Liouville section - there are an uncountable numbers of such numbers: simply make up more s like this

where the sequence { } is chosen as in the Liouville section, and etc .

In fact, for any fixed > 2, there are uncountably many real numbers such that each of them has infinitely many rational approximations satisfying

< ... ( )

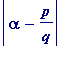A Measure Theory motivated question. So, there are uncountably many s satisfying the previous inequality, but how much space do they take up on the number line?

Immediate answer. Let be the set of all real numbers for which inequality ( ) has an infinite number of rational solutions, then [although appears to be large, and certainly is from a cardinality point of view; in fact it has the same cardinality as the entire real line!] has Lebesgue measuere zero [and so appears to be quite small ].

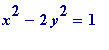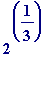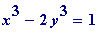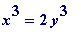Another question. Earlier it was observed that the equation having an infinite number of solutions in (positive) integers x , y is a natural outcome of observing that is irrational; what happens if one replaces (e.g.) the irrational number with the irrational number , and what then is the effect on the equation (since there are no (positive) integers x, y such that , and so the next best thing is to have 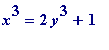, i.e., )

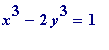Every such x , y would create a rational number so close to 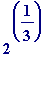as to almost be a solution of the inequality

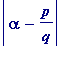< ... (iii)

By Liouville's theorem all such x , y must satisfy the inequality

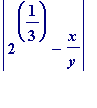> , for some constant c

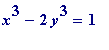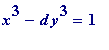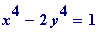A big question then is: Does/doesn't the equation (and others like it: , general non-cube d , , etc) have any solutions in integers x , y , and if so does it have infinitely many?

An answer. We are now getting into very, very deep water, and an answer will have to wait until we get to the Axel Thue section.