Complex roots of unity

School pupils familiar with complex numbers and DeMoivre's theorem know examples of algebraic numbers. For let 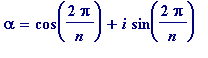alpha = cos(2*Pi/n)+i*sin(2*Pi/n) (where n is any natural number), then

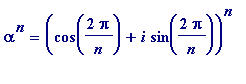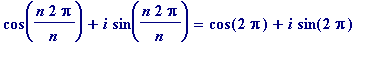alpha^n = (cos(2*Pi/n)+i*sin(2*Pi/n))^n = cos(n*2*Pi/n)+i*sin(n*2*Pi/n) = cos(2*Pi)+i*sin(2*P... = 1

and thus x = alpha is a solution of the polynomial equation x^n-1 = 0 .

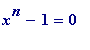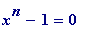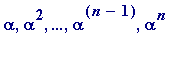In fact, the n solutions of the equation x^n-1 = 0 are alpha, alpha^2, `...`, alpha^(n-1), alpha^n (=1).

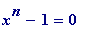For example, when n = 6 , the equation x^n-1 = 0 has 6 (algebraic number) solutions:

  • one of which will be of degree 1
  • another of which will also be of degree 1
  • two of which will be of degree 2
  • and another two of which will also be of degree 2

> n := 6:
factor(x^n - 1);

(x-1)*(x+1)*(x^2+x+1)*(x^2-x+1)

>

whereas, for example, when n = 7 , something quite different will happen (and I will not elaborate...):

> n := 7:
factor(x^n - 1);

(x-1)*(x^6+x^5+x^4+x^3+x^2+x+1)

>

Contact details 

After August 31st 2007 please use the following Gmail address: jbcosgrave at gmail.com

This page was last updated 18 February 2005 15:09:55 -0000