The meaning of 'linearly independent over the integers/rationals'
Later, if you read the Roth section, and then the Schmidt and Baker sections, there is a standard expression you will encounter: '... linearly independent over the rationals' (which is equivalent in meaning to ' linearly independent over the integers' ). I would like to explain what that expression means, because without understanding the meaning of this expression one cannot begin to appreciate the significance of the use of it in the Roth, Schmidt and Baker sections.
Choose any irrational number
A
. Then, infinitely many other numbers are irrational as a
consequence
. For example 2
A
, 3
A
, -4
A
,
![]() ,
,
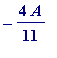 , ... are
all irrational
. What numbers are being suggested there? Simply
non-zero rational multiples
of
A
. Thus, e.g.,
, ... are
all irrational
. What numbers are being suggested there? Simply
non-zero rational multiples
of
A
. Thus, e.g.,
![]() is (trivially) irrational, for if not, we would have
is (trivially) irrational, for if not, we would have
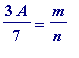 for some integers m and n (
for some integers m and n (
![]() ), giving
), giving
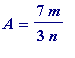 , is rational, whereas
A
is irrational.
, is rational, whereas
A
is irrational.
Now - to make a point - I choose two irrational numbers, two old friends
![]() and
and
![]() , and ask: could it be that
, and ask: could it be that
![]() is irrational as a
simple
consequence
is irrational as a
simple
consequence
![]() 's irrationality. Meaning? Could it be that
's irrationality. Meaning? Could it be that
![]() is a
rational
multiple of
is a
rational
multiple of
![]() ? Well it isn't (and a novice might like to wonder:
why not?
). Neither of course is
? Well it isn't (and a novice might like to wonder:
why not?
). Neither of course is
![]() a rational multiple of
a rational multiple of
![]() .
.
Whereas if I had chosen as my two irrationals (e.g.)
![]() and
and
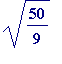 , then here each is irrational as a
simple
consequence of the other:
, then here each is irrational as a
simple
consequence of the other:
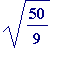 is
is
![]() .
.
![]() , and equally
, and equally
![]() is
is
![]() .
.
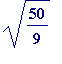 .
.
The (standard) expression that is used to summarise what I've just pointed out is to say that:
-
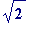 and
and
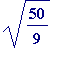 are
linearly dependent
over the rationals
(or integers)
are
linearly dependent
over the rationals
(or integers)
-
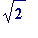 and
and
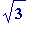 are
linearly
in
dependent over the rationals
(or integers)
are
linearly
in
dependent over the rationals
(or integers)
Formal definition. Let
![]() be
n
(real or complex) numbers (above
n
= 2), then
be
n
(real or complex) numbers (above
n
= 2), then
![]() are said to be
linearly dependent over the rationals
(equivalently integers) if there are
rational
numbers
are said to be
linearly dependent over the rationals
(equivalently integers) if there are
rational
numbers
![]() -
not all zero
- such that
-
not all zero
- such that
![]() . If
. If
![]() are
not
linearly dependent over the rationals then they are said to be linearly independent over the rationals.
are
not
linearly dependent over the rationals then they are said to be linearly independent over the rationals.
Example 1.
![]() and
and
![alpha[2] = sqrt(50/9)](images/transcendental123.gif) are linearly dependent
over the rationals since we have
are linearly dependent
over the rationals since we have
![alpha[1] = 3*alpha[2]/5](images/transcendental124.gif) , and thus
, and thus
![alpha[1]-3*alpha[2]/5 = 0](images/transcendental125.gif) (so
(so
![]() and
and
![]() may be chosen to be the rationals 1 and
may be chosen to be the rationals 1 and
![]() , but equally they could be chosen to be the integers 5 and
, but equally they could be chosen to be the integers 5 and
![]() .
.
Example 2 (exercise).
![]() and
and
![]() are linearly dependent
over the rationals (and notice it doesn't matter what is the base of the logarithms).
are linearly dependent
over the rationals (and notice it doesn't matter what is the base of the logarithms).
Example 3.
![]() and
and
![]() are
linearly independent
over the rationals
. For if not, then
are
linearly independent
over the rationals
. For if not, then
![]() for some rationals
for some rationals
![]() , not both zero. But then
, not both zero. But then
+log[10](7^r[2]) = 0](images/transcendental136.gif) ,
,
 = 0](images/transcendental137.gif) , giving
, giving
![5^r[1]*7^r[2] = 1](images/transcendental138.gif) , which is impossible (why?) except for
, which is impossible (why?) except for
![]() both
being zero.
both
being zero.
Example 4 (exercise).
![]() ,
,
![]() and
and
![]() are
linearly dependent
over the rationals
.
are
linearly dependent
over the rationals
.
I now make one last elementary point. First, return to the the earlier 'Choose any irrational number
A
...', and note that not only is any non-zero rational multiple of
A
irrational, but so also is
any such number
plus any rational number (positive, negative, or (trivially) 0). Thus, e.g.,
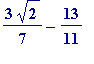 is irrational (why?)
is irrational (why?)
Now recall that the two irrationals
![]() and
and
![]() are essentially different, in that neither's irrationality is a simple consequence of the other because they are (the clarifying) 'linearly independent over the rationals'. But note that while (the similar looking)
are essentially different, in that neither's irrationality is a simple consequence of the other because they are (the clarifying) 'linearly independent over the rationals'. But note that while (the similar looking)
![alpha[1] = 3/4+2*sqrt(2)/5](images/transcendental146.gif) and
and
![alpha[2] = 6/7-9*sqrt(2)/11](images/transcendental147.gif) are both irrational (why?), they are linearly independent over the rationals (why?), and so neither is irrational as an
immediate
consequence of the other's irrationality. However their respective irrationalities are intimately linked to each other in that although neither is a
direct
rational multiple of the other, each however is obtainable from the other by the process I've just outlined: multiply by some non-zero rational, and add some other rational to that. In other words:
are both irrational (why?), they are linearly independent over the rationals (why?), and so neither is irrational as an
immediate
consequence of the other's irrationality. However their respective irrationalities are intimately linked to each other in that although neither is a
direct
rational multiple of the other, each however is obtainable from the other by the process I've just outlined: multiply by some non-zero rational, and add some other rational to that. In other words:
-
![alpha[2] = a[1]*alpha[1]+a[2]](images/transcendental148.gif) for some rational numbers
for some rational numbers
![a[1], a[2]](images/transcendental149.gif) , or equivalently
, or equivalently
-
![alpha[1] = b[1]*alpha[2]+b[2]](images/transcendental150.gif) for some rational numbers
for some rational numbers
![b[1], b[2]](images/transcendental151.gif)
These may be succinctly sumarised by noting that what we are
really saying
here is that the three numbers
![]() are linearly dependent over the rationals; that is there are rational numbers
are linearly dependent over the rationals; that is there are rational numbers
![]() - not all zero - such that
- not all zero - such that
![]() .
.
I would hope that when you see the proper contexts - the relevant parts of the Roth, Schmidt and Baker sections - these definitions will become more than mere definitions, and make perfect sense .