And a brief return to 'exceptional' primes 

Here I really will be brief and to the point. 

Earlier I remarked that we had an early criterion for a prime being 'exceptional' (in the context of quarter Gauss factorials, but indeed more generally), and that we had established to be the only (initial, meaning at ) exceptional prime up to . 

It would take me too far afield if I was to outline the meaning of higher exceptionality, but taking the notion of general -exceptionality as a given (what you encountered earlier was the case ) we later arrived at the following theorem  

(which is Theorem 9 of our paper #9 at https://www.johnbcosgrave.com/publications): 

a prime is -exceptional (for Gauss factorial quarter intervals) if and only if: 

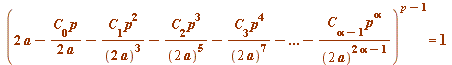(mod ) 

(where '' has its usual meaning, as throughout this talk)  

and thus, in particular at , a prime is -exceptional if and only if: 

(mod ) 

And finally I show you that test applied to all such primes up to 50,000: 

>

st:= time[real](): for p from 5 by 4 to 50000 do if isprime(p) then                         a||p := a_sign(p): if (2*a||p - p/(2*a||p))&^(p-1) mod p^2 = 1 then print(``); lprint(`The prime`, p, `is 1-exceptional for Gauss quarter factorials.`) fi fi od: print(``); lprint(`That computation took`, time[real]() - st, `seconds.`);

 

 

 

 

`The prime`, 29789, `is 1-exceptional for Gauss quarter factorials.`
`That computation took`, .735, `seconds.`

 

>

 

That was not the best application of the test - a much facter one is what we used - but a full explanation would take us further afield. 

_________________