And the continuation, and finalisation 

The obvious question to pursue then was this: what can one say about the next object up (as it were), namely: (mod )  

Thus, what is the correct shape of the following possible extension: 

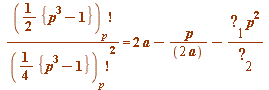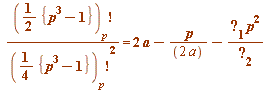(mod )

(mod ) 

What might the unknows and be (the last sign is not important; yes, it could have been 'plus', but then ... )?  

There are a couple of candidates for , but an obvious candidate was , and so we ran with: 

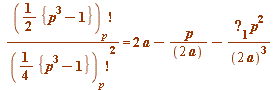(mod ) 

which of course gave that (a possible) would be given by the (mod ) evaluation of the following right-hand side: 

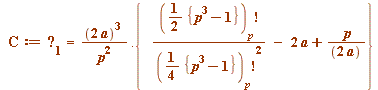
And here is that (exciting!) computation for primes up to 41:
 

>

L := []: for p from 5 by 4 to 41 do if isprime(p) then L := [op(L), p] fi od: for p in L do                       a||p := a_sign(p):                       A||p := 2*a||p:                     NUM||p := PI(p^3, 2, 1):                     DEN||p := PI(p^3, 4, 1):                     LHS||p := mods(NUM||p/DEN||p^2, p^3):                       C||p := (A||p - p/A||p - LHS||p) * (A||p^3/p^2);           od: print(``); print(array([['p', ``, ``, 'C'], seq([p, ``, ``, mods(C||p, p)], p = L)])): print(``);

 

 

 

	(11.1)

 

>

 

which strongly suggested that we had this new congruence: 

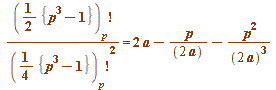(mod ) 

And now I speed up: what might '' be in a possible: 

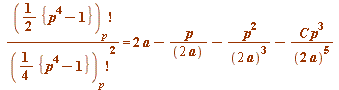(mod ) 

So, we computed a (mod ) evaluation of the following right-hand side: 

And here it is (note all the appropriately changed powers etc): 

>

L := []: for p from 5 by 4 to 29 do if isprime(p) then L := [op(L), p] fi od: for p in L do                   a||p := a_sign(p):                   A||p := 2*a||p:                 NUM||p := PI(p^4, 2, 1):                 DEN||p := PI(p^4, 4, 1):                 LHS||p := mods(NUM||p/DEN||p^2, p^4):                   C||p := (A||p - p/A||p - p^2/A||p^3 - LHS||p) * (A||p^5/p^3);           od: print(``); print(array([['p', ``, ``, 'C'], seq([p, ``, ``, mods(C||p, p)], p = L)])): print(``);

 

 

 

	(11.2)

 

>

 

>

 

which strongly suggested that we had this new congruence: 

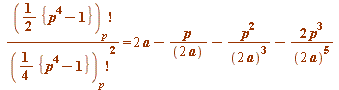(mod ) 

In my talk I asked for guesses for a possible value of in this possible congruence: 

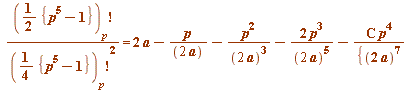(mod ) 

(You will recall your responses ... )  

(Once, in BYU (Utah), someone suggested the emerging coefficients could be the Fibonacci numbers: 1, 1, 2, 3, 5, 8, ... ) 

(Just once, in Galway, someone correctly guessed (a fluke, of course) what's coming up: ) 

And, it emerged that these successive possible -values proved to be: the Catalan numbers: 

where is given by: 

,  

A good internet source is https://en.wikipedia.org/wiki/Catalan_number. 

Here are the early ones: 

>	print(``); seq(binomial(2*n, n)/(n+1), n = 0..20);

 

 

	(11.3)

 

>

 

So that our discovery was: 

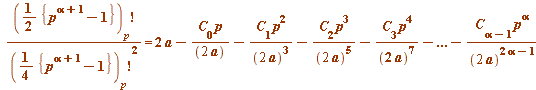(mod ) 

This is Theorem 7 of our mod p^3 Acta Arithmetica paper of 2010. 

Besides this we also obtained a similar congruence in connection with Jacobi's binomial coefficient congruence, one which Jacobi obtained in 1837, while Gauss was still alive (did Gauss try, but fail to obtain it?)