(the order values appear to go:  

>

p := 5: bound := 6:  for alpha to bound do           GF||alpha := PI(p^alpha, 4, 1):          ord||alpha := order(GF||alpha, p^alpha):        od: print(``); print(array([ ['p', ``, 'alpha', ``, ``, 'p^alpha', ``, ``, '(({p^alpha-1}/4))[p]!', ORDER], seq([p, ``, alpha, ``, ``, ifactor(p^alpha), ``, ``, GF||alpha, ifactor(ord||alpha)], alpha = 1..bound)])): print(``);

 

 

 

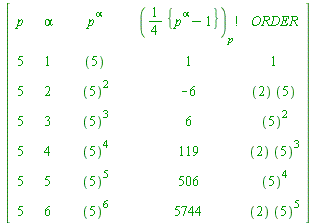	(9.2.1.1)

 

>	gamma, 2*gamma*p, gamma*p^2, 2*gamma*p^3, `...`;

 

(9.2.1.2)

 

>