Title, speaker, aim/structure of talk 

Title of talk. The classic 'binomial coefficient congruence' of Gauss, and more besides ...
A talk given to the Student Mathematics Society (Trinity College Dublin)
Wednesday March 2017Speaker. John B. Cosgrave ([email protected], web site www.johnbcosgrave.com) 

                                          joint work with Karl Dilcher (http://www.mathstat.dal.ca/~dilcher/) 

Aim/structure of talk. Here are the main points (I should point out that I am cutting many corners in this presentation): 

• A beautiful classic work of Gauss: his binomial coefficient congruence (1828, when Gauss was 51), and an extension of this work - "proposed by F. Beukers" - proved by Chowla, Dwork and Evans (1986).
  
  All of this requires a brief survey of some earlier classic, well-known work (Fermat, Wilson, Lagrange, ... )
  
  

• Next, in 2007, Karl Dilcher and I began a study of what we termed "Gauss factorials", in connection with which we examined these very special ones (whose meaning will be clear later):
  
  
                                                                            ,  
  

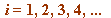
• specifically their (what could be called) "gamma-structure", meaning the behaviour of the sequence of integers:
  
                                                                       
  

• and, in attempting (successfully, up to a point) to understand the latter, and then combined with Chowla-Dwork-Evans we were led to ...

_________________
 

Finally I will quickly show how the latter subsequently fed back into our gamma-structure work in connection with "exceptional primes" 

There are several beautifully organised slide talks by Karl, and one video, at