An RSA public -key ( digital signature ) demonstration

Here, with time as the enemy, I can only convey the essential spirit of the basic RSA idea.

Suppose 'Alice' wishes to send a message ("Hi Bob, let's meet. Alice") to Bob; then not only can she do so - in a manner similar to that you have already seen in the PH example - but she can give him a gaurantee that she really is the author of the message (her digital signature comes into play here...)

Important note. Her message to him is NOT a secure one, in the sense that anyone who intercepts her message, and who knows her public -key, may then read her message to Bob. Also, although he can also send her a message (using her public-key) - perhaps 'Thanks Alice. Where? When? Bob' - she however can have no gaurantee that he was the author, since some impostor - knowing her public-key - could have sent it.

(In case, as a novice, my reader objects along the lines of ' why bother with all of this public and private key stuff, why not just keep the keys secret and save a lot of bother... ', well that brings up a whole host of problems - not least the so-called transportation problem (how - in a crisis - can one securely deliver secret keys over a distance?) which I could not even begin to discuss here...)

First of all Alice chooses two 'large' primes (throwing caution to the winds):

> pA := nextprime(10^60 + 1234567*rand()^5);

> qA := nextprime(10^65 + 8765439999*rand()^5);

>

forms their product (her public modulus, which she will use with her private ' d ', constructed in a moment):

> nA := pA*qA;

>

computes the 'Euler phi-value' of the integer nA (that integer plays the same role in the RSA method as ( ) did in the PH case, and I ask my reader to note the apparently trivial remark that its calculation requires knowing ' pA ' and ' qA ' ):

> phi_nA := (pA - 1)*(qA - 1);

>

Next Alice chooses an encryption power:

> eA := nextprime(10^25 + rand()^2);

>

Let's check if that the requirement gcd( eA , ( )( )) = 1 holds (there is only a very remote possibility that it doesn't, and I leave it to you to think about why that is):

> igcd(eA, phi_nA);

>

and computes her private -decryption power dA:

> igcdex(eA, phi_nA, 'xA', 'yA'):
dA := xA mod phi_nA; # Step 3, finding 'dA'

>

See in passing that the product of eA and dA does leave remainder 1 on division by ( )( ):

> eA*dA mod (pA - 1)*(qA - 1);

>

Alice's public and private keys are then ( eA , nA ) and ( dA , nA ) (in the 'real world', a 'Certification Authority' is the guarantor that ( eA , nA ) is her 'public-key').

>

Next, Alice converts her message to a number:

> ANUM := to_number(`Hi Bob, let's meet. Alice`);

>

Alice then encrypts ANUM by using her private decryption power ( that is her digital signature ):

• She computes the remainder 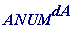leaves on division by n
  

I'll call the resulting number ASEND , since it's that number Alice sends to Bob.

> ASEND := ANUM&^dA mod nA;

>

Let us observe the text equivalent of that encrypted number is just meaningless junk; I may have to recompute with another ' n ' should there be a '00' in that string in the wrong position):

> from_number(ASEND);

>

Bob then reads Alice's message by (removing the disuising coat of paint as it were, using Alice's public paint):

• Computing the remainder that leaves on division by n

The mathematics of two-prime version of Fermat's little theorem gaurantees that the outcome is the numerical form of the original text:

> BSEE := ASEND&^eA mod nA;

> from_number(BSEE);

>

Two quick points, of which the first is fundamental :

• SECURITY. Unlike the PH, private-key method, where the keys had to be kept secret, here Alice's private-key is safe and secure , even though her other key is allowed to be in the public domain. (The big question is: WHY?... One might naively think as follows: knowing ' n ' and ' e ', surely one could impersonate Alice by calculating ' d ' through factoring n , thus know ' p ' and ' q ', and so compute ' d ' from requirement #3 (as in the PH case). Ah!! There's the rub:
  
  FACTORING - IN GENERAL - IS HARD!!! )
  
• SIZE OF TEXT. Here - as in the PH case - if the numerical form of the text is greater than n , then it must be broken down into sections each having numerical value less than n (for a similar reason...)