(the Euler phi-value of n ), if I have time...

I would like to touch briefly on that critical "phi_n" ( my notation above). - the Euler phi function - came on the mathematical scene through Euler's classic generalization of Fermat's little theorem (I have devoted an entire section of my web site - with my personal year-2001 homage-lecture to mark the 400th anniversary of Fermat's birth - to that classic theorem):
Fermat's little theorem. Let p be prime, and a be any integer not divisible by p , then 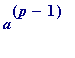leaves remainder 1 on division by p .

Euler's generalization of Fermat's theorem. Let n be any natural number ( , prime or otherwise), and a be any integer such that gcd( a , n ) = 1, then 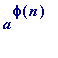leaves remainder 1 on division by n (where is the number of integers between 1 and ( ) that share no common factor, greater than 1 , with n ).

Euler's beautiful formula for . = n , where the product is evaluated over the distinct prime divisors , ... of n .

Two examples only:

1. When n = p , is itself a prime, = = 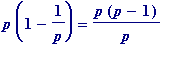, the ' ' of
Fermat's little theorem.

2. When n = pq , the product of two distinct primes,

= = ,

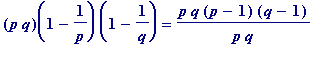the ' ' of the RSA method.

Maple has a command for computing (it requires loading Maple's Number Theory package; the items are alphabetically listed, and 'phi' is just after 'pdexpand')

> with(numtheory);

Warning, the protected name order has been redefined and unprotected

> phi(13);

> phi(15);

> phi(25);

> phi(12345678910987654321);

>

> p[1] := nextprime(1234);

> q[1] := nextprime(5678);

> n[1] := p[1]*q[1];

> n[1]*(1 - 1/p[1])*(1 - 1/q[1]); # Euler formula

> phi(n[1]); # Maple command

>

But what about, say:

> p[2] := nextprime(10^24 + rand()^2);

> length(p[2]);

> q[2] := nextprime(10^29 + 54321*rand()^2);

> length(q[2]);

> n[2] := p[2]*q[2];

>

Here NOW - I hope - you will see the difference:

> n[2]*(1 - 1/p[2])*(1 - 1/q[2]); # Euler formula

BUT FOR:

> # phi(n[2]);

the computation clock comes on... Maple cannot quickly compute because - to do so - it needs to factor in order to find and , to use Euler's formula to evaluate , and here they have only 25 and 30 digits... That should explain to you why earlier I had to define 'phi_nA' (with the known values of pA and qA) in the RSA demonstration: Maple could not itself have carried out the computation had I used phi(nA)...