> # Fermat's 2-squares.mws
Note to anyone reading this on the web in html format. Not having Maple you may not be familiar with its use of Sections (where you see those [+]s). To read the contents of a section, simply click on the [+] and it will expand into a [-], and you will see text, plus calculations (of course you cannot change the calculations, as you could with the active Maple worksheet). Later, by scrolling back up, you may close the box by clicking on the [-].
Title
Fermat's 2-squares theorem
(proved here using the
Dirichlet box principle
,
together with an idea of Axel Thue
)
Remark (aimed at number theorists who might read this) on the approach I've adopted here
. The proof that I give here of Fermat's 2-squares theorem (as part of my 3rd year (BA only) course
Challenging Mathematical Puzzles and Problems
) is most certainly not the best, nor the most insightful proof there is of Fermat's theorem; and the proof given here serves mainly to demonstrate a
particular use
(the Thue result) of the entirely elementary, but quite profound, Dirichlet box principle (where would the work of - say - Roth or Schmidt be without it?!) which my students will encounter is less demanding areas (e.g. Choose any (
![]() ) integers from [1, 2, 3, 4, ... , (
) integers from [1, 2, 3, 4, ... , (
![]() ),
),
![]() ], then one of those divides another (different!) one of those. Prove.)
], then one of those divides another (different!) one of those. Prove.)
If you don't have Maple, and are reading this in html format then, of course, you won't be able to execute your own commands, but if you do have Maple then you may make your own changes to value assignments.
Introduction to Fermat's 2-squares theorem ( how it came about)
One of the great classic theorems of Number Theory is the 'Fermat 2-square theorem' which states that every prime leaving remainder 1 on division by 4 is a sum of two squares of integers (a unique sum, in fact, if one ignores change of sign, or interchange of values). It is easy to see how he found / discovered this theorem (or more precisely came to suspect it was true, for he couldn't prove it), since he knew of the Greek result (due to Diophantus) giving all possible integer-sided right-angled triangles: Let x , y and z be integer (positive, of course) sides of a right-angled triangle, with z (the length of) the hypothenuse ; then x , y , and z are given by
(
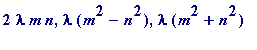 )
)
for some (positive) integers
![]() (
lambda
),
m
and
n
, with
(
lambda
),
m
and
n
, with
-
m
and
n
of 'opposite parity' (meaning one of them is
even
, the other
odd
),
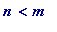 , and
, and
-
m
and
n
are 'relatively prime' (meaning there is no prime that divides both of them: i.e.
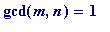 )
)
Remark
. The last two conditions
make
the triple (
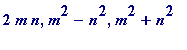 ) form the sides of a
primitive
right-angled triangle (here 'primitive' means the formed triangle is not an integer 'multiple' of a
smaller
integer-sided right-angled triangle (in the way that - for example - (6, 8, 10) - where
) form the sides of a
primitive
right-angled triangle (here 'primitive' means the formed triangle is not an integer 'multiple' of a
smaller
integer-sided right-angled triangle (in the way that - for example - (6, 8, 10) - where
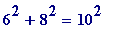 - is simply the 'double' of the triangle with sides (3, 4, 5) (where
- is simply the 'double' of the triangle with sides (3, 4, 5) (where
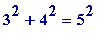 ).
).
Trivial exercise
. Verify that the numbers in the triple (
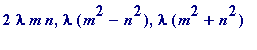 )
do
form the sides of a right-angled triangle.
)
do
form the sides of a right-angled triangle.
Primitive right-angled triangles (with particular attention being given to the hypothenuse , underlined ). Here are some xs , y s and z s forming (or not forming) the sides of primitive right-angled triangles:
-
(3, 4,
5
) (or (4, 3,
5
), we're not fussed about the
order
of the
two shorter sides) coming from the choice ( m , n ) = (2, 1) - (8, 15, 17 ) coming from the choice ( m , n ) = (4, 1)
-
(24, 7,
25
) coming from the choice (
m
,
n
) = (4, 3)
but not - say - the choice ( m , n ) = (3, 1), which -
although
(
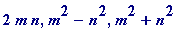 ) is (8, 6, 10) - and
) is (8, 6, 10) - and
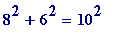 , does not produce a primitive right-angled triangle (the '3
' and '1' being of the same parity makes the sides all be even (thus divisible by 2, and so - in this case - is a multiple of the 'smaller' triangle (3, 4, 5)),
, does not produce a primitive right-angled triangle (the '3
' and '1' being of the same parity makes the sides all be even (thus divisible by 2, and so - in this case - is a multiple of the 'smaller' triangle (3, 4, 5)),
nor - say - the choice ( m , n ) = (9, 6), which -
although
(
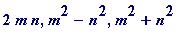 ) is (108, 45, 117) - and
) is (108, 45, 117) - and
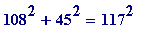 , does not produce a primitive right-angled triangle (here the '9
' and '6'
are
of the opposite,
but now
they are both divisible by 3 which makes the sides be divisible by 3 (in fact by 9, and - in this case - is a multiple of the 'smaller' triangle (12, 5, 13))
, does not produce a primitive right-angled triangle (here the '9
' and '6'
are
of the opposite,
but now
they are both divisible by 3 which makes the sides be divisible by 3 (in fact by 9, and - in this case - is a multiple of the 'smaller' triangle (12, 5, 13))
A question that Fermat asked himself . Which numbers occur as the hypothenuse of an (integer-sided) right-angled triangle?
The obvious thing to do (as always) is to do some calculating
. Asking the question: for which integers ('
h
' say),
is
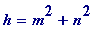 for some
m
and
n
subject to the two conditions above, trial and error quickly uncovers the early values of such
h
s:
for some
m
and
n
subject to the two conditions above, trial and error quickly uncovers the early values of such
h
s:
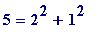 (
m
,
n
are even, odd),
(
m
,
n
are even, odd),
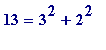 (
m
,
n
are odd, even),
(
m
,
n
are odd, even),
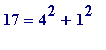 (
m
,
n
are even, odd),
(
m
,
n
are even, odd),
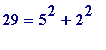 (
m
,
n
are odd, even),
(
m
,
n
are odd, even),
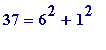 (
m
,
n
are even, odd),
(
m
,
n
are even, odd),
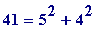 (
m
,
n
are odd, even),
(
m
,
n
are odd, even),
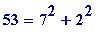 (
m
,
n
are odd, even),
(
m
,
n
are odd, even),
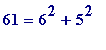 (
m
,
n
are even, odd),
(
m
,
n
are even, odd),
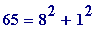 (
m
,
n
are even, odd), etc ...
(
m
,
n
are even, odd), etc ...
A numerically sensitive person would
notice
, but
not be surprised
(why?) by the occurence of
so
many
(
but not all
)
primes
(and would, of course, notice that '65'...), and would begin to wonder about a new:
Question
. Which
primes
are a sum of two integers? This is what one finds:
-
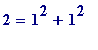 is a sum of two squares (but does not, of course, lead to a primitive right-angled triangle because...)
is a sum of two squares (but does not, of course, lead to a primitive right-angled triangle because...)
- none of 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, ... is a sum of two squares
- each of 5, 13, 17, 29, 37, 41, 53, 61, 73, ... is a sum of two squares
and then the next obvious
Question . What is it that distinguishes the last two sets of primes from each other? It was Fermat's great good fortune to notice that
- the former all left remainder 3 on division by 4 (or at least did so as far as calculated...), while
- the latter all left remainder 1 on division by 4 (or at least did so as far as calculated...)
It is entirely elementary to prove that
no
integer
n
(whether prime or not) with
![]() (mod 4) is a sum of two squares of integers, but that left Fermat wondering if
every
prime
p
,
(mod 4) is a sum of two squares of integers, but that left Fermat wondering if
every
prime
p
,
![]() (mod 4), is a sum of two squares of integers (and here one should bear this in mind: it is
not
true that
every
integer
n
with
(mod 4), is a sum of two squares of integers (and here one should bear this in mind: it is
not
true that
every
integer
n
with
![]() (mod 4) is a sum of two squares of integers. Examples are
(mod 4) is a sum of two squares of integers. Examples are
![]() , ... ). Fermat couldn't prove his discovery, and it had to wait until the following century when Euler gave the first proof. Many others have been created in the following centuries. The proof that I give here (I don't know who put it together (I think it was in a book of Sierpinski's that I first read it, forty years ago) combines two ideas, which we meet in the next two sections.
, ... ). Fermat couldn't prove his discovery, and it had to wait until the following century when Euler gave the first proof. Many others have been created in the following centuries. The proof that I give here (I don't know who put it together (I think it was in a book of Sierpinski's that I first read it, forty years ago) combines two ideas, which we meet in the next two sections.
A special property of primes
p
,
![]() (mod 4) (we use
Wilson's theorem
)
(mod 4) (we use
Wilson's theorem
)
Theorem 1 (the special property)
. For every prime
p
with
![]() (mod 4) there is an integer
a
such that
(mod 4) there is an integer
a
such that
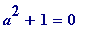 (mod
p
). (In fact there are always
exactly two
such (mutually incongruent)
a
's.)
(mod
p
). (In fact there are always
exactly two
such (mutually incongruent)
a
's.)
Trying some by hand .
For
![]() , one finds that
, one finds that
![]() will do [
will do [
![]() is the other one]
is the other one]
For
![]() , one finds that
, one finds that
![]() will do [
will do [
![]() is the other one]
is the other one]
For
![]() , one finds that
, one finds that
![]() will do [
will do [
![]() is the other one]
is the other one]
For
![]() , one finds that
, one finds that
![]() will do [
will do [
![]() is the other one] etc ...
is the other one] etc ...
Of course a Maple command that will find such a 's is msolve:
> msolve(a^2 + 1 = 0, 5);
![]()
> msolve(a^2 + 1 = 0, 13);
![]()
> msolve(a^2 + 1 = 0, 17);
![]()
>
for p from 5 by 4 to 100 do
if isprime(p)
then print([p, msolve(a^2 + 1 = 0, p)])
fi
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
There are many ways of proving this famous theorem, and one very quick way to do it (I know it will appear very much like a 'rabbit out of a hat', but we won't have time to divert too much) is to make use of another famous theorem, Wilson's theorem (whose proof I will not give here. Incidentally there are - as is often the case in Number Theory - many different proofs of this, one of which is my own, published in the UK Mathematical Gazette in February 1967).
Wilson's theorem (which I will not be proving here)
. For every prime
p
one has
![]() (mod
p
).
(mod
p
).
Examples .
When
![]() ,
,
![]() =
=
![]() (mod 5)
(mod 5)
When
![]() ,
,
![]() =
=
![]() (mod 11)
(mod 11)
When
![]() ,
,
![]() =
=
![]() (mod 13)
(mod 13)
Remark
. Recall (from your second year studies that when proving Fermat's 'little' theorem one got to a point where one had (with
p
prime and
![]() (mod
p
):
(mod
p
):
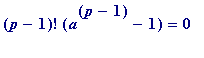 (mod
p
)
(mod
p
)
and then continued by saying that
either
![]() (mod
p
)
or
(mod
p
)
or
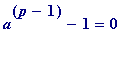 (mod
p
). Then one argued that
(mod
p
). Then one argued that
![]() (mod
p
) and thus ... giving Fermat's little theorem. SO: that '
(mod
p
) and thus ... giving Fermat's little theorem. SO: that '
![]() ' is not congruent to 0 mod
p
, ... and it is only if one had the curiousity to
wonder
- what (if anything)
is
it congruent to mod
p
? - that one could have
discovered
'Wilson's theorem'...
' is not congruent to 0 mod
p
, ... and it is only if one had the curiousity to
wonder
- what (if anything)
is
it congruent to mod
p
? - that one could have
discovered
'Wilson's theorem'...
In the following I am not concerned by the
inefficient
computation of of
![]() mod
p
, nor later when I have a look at
mod
p
, nor later when I have a look at
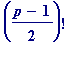 mod
p
.
mod
p
.
>
for p to 30 do
if isprime(p)
then print(p, (p-1)!, mods((p-1)!, p))
fi
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Here now is the simple idea that enables one to prove Theorem 1 above, by using Wilson's theorem, which I will first illustrate with the prime
![]() : first note that we have
: first note that we have
![]() (mod 13), and then - noting that
(mod 13), and then - noting that
![]() (mod 13),
(mod 13),
![]() (mod 13),
(mod 13),
![]() (mod 13),
(mod 13),
![]() (mod 13),
(mod 13),
![]() (mod 13),
(mod 13),
![]() (mod 13), we obtain
(mod 13), we obtain
![]() = 12.11.10.9.8.7.6.5.4.3.2.1 =
= 12.11.10.9.8.7.6.5.4.3.2.1 =
![]() .6.5.4.3.2.1 = -1 (mod 13)
.6.5.4.3.2.1 = -1 (mod 13)
and thus
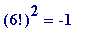 (mod 13) (namely
(mod 13) (namely
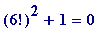 mod 13). Thus a working value for the claimed '
a
' of the theorem is whatever number one gets from calculation 6! mod 13:
mod 13). Thus a working value for the claimed '
a
' of the theorem is whatever number one gets from calculation 6! mod 13:
> a := 6! mod 13;
![]()
> a^2 + 1 mod 13;
![]()
You should see
why
that then 'works' in the general case, and
what
is the
relevance
of
![]() (mod 4).
(mod 4).
A famous unsolved problem in connection with this
. The above clever trick of replacing the end remainders with their negatives can also be done with primes
p
,
![]() (mod 4), and there - instead of getting an '
a
' with
(mod 4), and there - instead of getting an '
a
' with
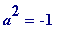 (mod
p
) - one gets an '
a
' with
(mod
p
) - one gets an '
a
' with
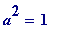 (mod
p
), in fact
(mod
p
), in fact
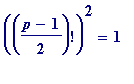 (mod
p
), and thus (why?)
(mod
p
), and thus (why?)
-
either
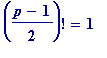 (mod
p
) (and this happens for
(mod
p
) (and this happens for
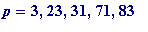 , ...
, ...
-
or
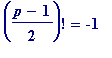 (mod
p
) (and this happens for
(mod
p
) (and this happens for
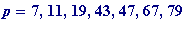 , ...
, ...
and it is an unsolved question as to what makes the remainder be PLUS 1, and what makes it be MINUS 1.
>
for p from 3 by 4 to 100 do
if isprime(p) and mods(((p-1)/2)!, p) = 1
then print([p, ((p-1)/2)!, 1])
elif isprime(p) and mods(((p-1)/2)!, p) = -1
then print([p, ((p-1)/2)!, -1])
fi
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A 2-variable congruence result of Thue's
Theorem
. Let
p
be
prime
and let
a
be any integer with
![]() (mod
p
), then there are integers
x
and
y
such that
(mod
p
), then there are integers
x
and
y
such that
![]() (mod
p
) with
(mod
p
) with
![]() and
and
![]() , and
, and
![]() , and
, and
![]() .
.
(Note in the proof that
p
's primality is used only at one small point. Also note that one could have '
![]() ' in place of '
' in place of '
![]() ' (though
different
pairs of values may result when the signs are changed), and later make the same use of the alternative version in the proof of the Fermat 2-squares theorem.)
' (though
different
pairs of values may result when the signs are changed), and later make the same use of the alternative version in the proof of the Fermat 2-squares theorem.)
Proof (which uses the Dirichlet box principle, and illustrated below)
. Let
![]() ('ceil' (the Maple command used below) for 'ceiling',
meaning
the integer satisfying
('ceil' (the Maple command used below) for 'ceiling',
meaning
the integer satisfying
![]() ,
,
![]() (in other words,
(in other words,
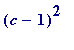 and
and
![]() are the squares
before
and
after
the prime
p
), and consider the
are the squares
before
and
after
the prime
p
), and consider the
![]() integers:
integers:
![]() , ... ,
, ... ,
![]() ,
,
![]() , ... ,
, ... ,
![]() ,
,
![]() , ... ,
, ... ,
![]() ,
,
... ...
![]() , ... ,
, ... ,
![]()
Since
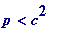 then - by the Dirichlet box principle -
some two
(at least) of those integers must be congruent mod
p
; that is, we have two
different
pairs (
then - by the Dirichlet box principle -
some two
(at least) of those integers must be congruent mod
p
; that is, we have two
different
pairs (
![]() ) and (
) and (
![]() ) such that
) such that
![]() (mod
p
) for some
(mod
p
) for some
![]() between 1 and
c
, and then
between 1 and
c
, and then
![]() (mod
p
) ... (i)
(mod
p
) ... (i)
Setting
![]() and
and
![]() we have
we have
![]() (mod
p
), and clearly
(mod
p
), and clearly
![]() and
and
![]() . (But could it be - horror of horrors!! - that all we've got for our efforts is the
trivial
. (But could it be - horror of horrors!! - that all we've got for our efforts is the
trivial
![]() (mod
p
); that's the last point to be settled:) Now
(mod
p
); that's the last point to be settled:) Now
![]() because, if not, we would have
because, if not, we would have
![]() and (i) would give
and (i) would give
![]() (mod
p
), giving
(mod
p
), giving
![]() (conflicting with (
(conflicting with (
![]() ) and (
) and (
![]() ) being different pairs). Also
) being different pairs). Also
![]() because, if not, we would have
because, if not, we would have
![]() and (i) would give
and (i) would give
![]() (mod
p
), giving
(mod
p
), giving
![]() (mod
p
) (since
p
is
prime
and
(mod
p
) (since
p
is
prime
and
![]() (mod
p
)), giving
(mod
p
)), giving
![]() (once again conflicting with (
(once again conflicting with (
![]() ) and (
) and (
![]() ) being different pairs). [
end of proof
]
) being different pairs). [
end of proof
]
Advice . As always, some hand-performed calculations help to reinforce the idea.
Maple illustrations of the Thue (Dirichlet) theorem
>
p := 23; a := 7; c := ceil(sqrt(p));
A := array(1..c,1..c):
for x to c do for y to c do
A[x, y] := a*x + y mod p;
od; od;
print(A);
lprint(`Note. There are`, c^2, `entries, and thus, on division by`, p,`there must be AT LEAST TWO entries that are congruent mod`, p);
![]()
![]()
![]()
![matrix([[8, 9, 10, 11, 12], [15, 16, 17, 18, 19], [...](images/Fermat-Thue 2-squares175.gif)
`Note. There are`, 25, `entries, and thus, on division by`, 23, `there must be AT LEAST TWO entries that are congruent mod`, 23
>
Looking at that Maple output one can see quite a few duplicates (3, 4, 5, 9, 10 and 11 in fact), and choosing any one of them - 9 say (the 2 nd in the 1 st row, and the 1 st in the 3 rd row) - one has:
![]() (mod 13)
(mod 13)
giving
![]() (mod 13)
(mod 13)
namely
![]() (mod 13)
(mod 13)
and so it produces an '
x
' and '
y
' of the theorem with
![]() and
and
![]() . And here's an example with a '0' (in fact two of them) in the
interior
of the table:
. And here's an example with a '0' (in fact two of them) in the
interior
of the table:
>
p := 13; a := 6; c := ceil(sqrt(p)); A := array(1..c,1..c):
for x to c do for y to c do
A[x, y] := a*x + y mod p;
od; od; print(A);
lprint(`Note. There are`, c^2, `entries, and thus, on division by`, p,`there must be AT LEAST TWO entries that are congruent mod`, p);
![]()
![]()
![]()
![matrix([[7, 8, 9, 10], [0, 1, 2, 3], [6, 7, 8, 9], ...](images/Fermat-Thue 2-squares184.gif)
`Note. There are`, 16, `entries, and thus, on division by`, 13, `there must be AT LEAST TWO entries that are congruent mod`, 13
>
That '0' in the 2nd row simply means that
![]() (mod 13) (and so
(mod 13) (and so
![]() ,
,
![]() satisfy the Theorem), or the '0' in the 4th row simply means that
satisfy the Theorem), or the '0' in the 4th row simply means that
![]() (mod 13).
(mod 13).
This result of Thue's makes no mention whatever of the value of
p
mod 4; it's true of
all
primes (but in the proof I give in the next section of the Fermat 2-squares theorem we will
need
to use that
![]() (mod 4)).
(mod 4)).
Here is one last example, this time with a prime that happens to be 3 (mod 4).
>
p := 79; a := 6; c := ceil(sqrt(p)); A := array(1..c,1..c):
for x to c do for y to c do
A[x, y] := a*x + y mod p;
od; od; print(A);
lprint(`Note. There are`, c^2, `entries, and thus, on division by`, p,`there must be AT LEAST TWO entries that are congruent mod`, p);
![]()
![]()
![]()
![matrix([[7, 8, 9, 10, 11, 12, 13, 14, 15], [13, 14,...](images/Fermat-Thue 2-squares193.gif)
`Note. There are`, 81, `entries, and thus, on division by`, 79, `there must be AT LEAST TWO entries that are congruent mod`, 79
>
You shouldn't be surprised - in any example (Maple or otherwise) - by the way the entries in the rows read from left to right...
Proof of the Fermat 2-square theorem
All (finally!) is now in place for:
Theorem
. Let
p
be any prime with
![]() (mod 4), then there are integers
x
and
y
such that
(mod 4), then there are integers
x
and
y
such that
 .
.
Proof
. Since
![]() (mod 4) then there exists an integer
a
such that
(mod 4) then there exists an integer
a
such that
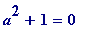 (mod
p
) ... (i)
(mod
p
) ... (i)
Also, there are integers x and y such that
![]() (mod
p
) ... (ii)
(mod
p
) ... (ii)
with
![]() and
and
![]() , and
, and
![]() and
and
![]() . Multiplying throughout (ii) by (
. Multiplying throughout (ii) by (
![]() ) gives
) gives
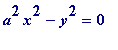 (mod
p
) ... (iii)
(mod
p
) ... (iii)
and throughout (i) by
![]() gives
gives
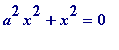 (mod
p
) ... (iv)
(mod
p
) ... (iv)
Subtracting (iii) from (iv) gives
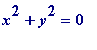 (mod
p
). Thus
(mod
p
). Thus
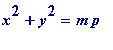 for
some
integer
m
(and our aim is to argue it MUST be 1 giving
for
some
integer
m
(and our aim is to argue it MUST be 1 giving
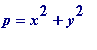 ). We have
). We have
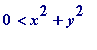 (even
only one
of
x
and
y
being non-zero would have gauranteed that) and so
(even
only one
of
x
and
y
being non-zero would have gauranteed that) and so
![]() , and since
, and since
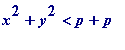 then
then
![]() , giving
, giving
![]() . Thus
m
is
1. [
end of proof
]
. Thus
m
is
1. [
end of proof
]
See the ' x ' and ' y ' generated by combining (Wilson), Thue and Dirichlet
Your understanding of the above may be enhanced by seeing the following calculations, which start with a prime
p
,
![]() (mod 4), and continue... I know primes that are 1 mod 4 off by heart, but if you want some such primes then do something like:
(mod 4), and continue... I know primes that are 1 mod 4 off by heart, but if you want some such primes then do something like:
>
for k from 150 to 200 do
if k mod 4 = 1 and isprime(k)
then print(k) fi od;
![]()
![]()
![]()
![]()
![]()
> p := 173; a := ((p-1)/2)!; a mod p; a^2 + 1 mod p;
![]()
![]()
![]()
![]()
![]()
>
Now to see (what one might call) the Thue table:
>
c := ceil(sqrt(p)); A := array(1..c,1..c):
for x to c do for y to c do
A[x, y] := a*x + y mod p;
od; od; print(A);
lprint(`Note. There are`, c^2, `entries, and thus, on division by`, p,`there must be AT LEAST TWO entries that are congruent mod`, p);
![]()
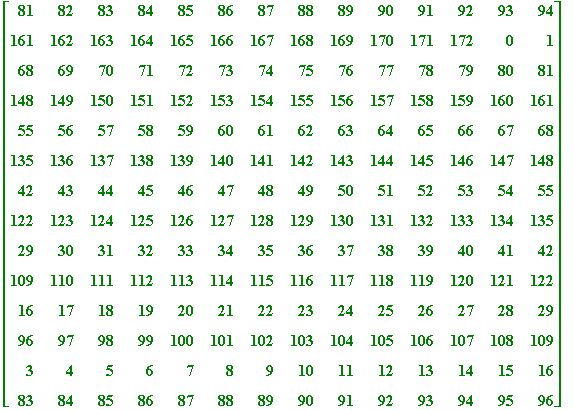
`Note. There are`, 196, `entries, and thus, on division by`, 173, `there must be AT LEAST TWO entries that are congruent mod`, 173
>
As it happens there is a convenient '0' that occurs in the table (so one doesn't have to look out for two repeated entries (like 130 and 130), and so we can immediately read off the ' x ' and ' y ' values. But if you're too lazy to count along the rows and columns to find the ' x ' and ' y ' values
>
for x to c do for y to c do
if A[x, y] = 0 then print(x, y, x^2+y^2)
fi od; od;
![]()
>
and so one sees that
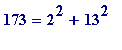 .
.
Much, much more can be done with these ideas
There is a great deal more that may be achieved in connection with the above ideas. For example one may prove in a similar fashion the following:
Theorem
. Let
p
be any prime with
![]() (mod 8) or
(mod 8) or
![]() (mod 8) then
(mod 8) then
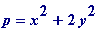 for some integers
x
and
y
.
for some integers
x
and
y
.
Examples
.
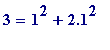 ,
,
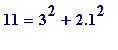 ,
,
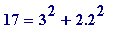 ,
,
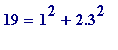 , ...
, ...
To give a proof, though, one needs to have access to another classic result: for every prime with
![]() (mod 8) or
(mod 8) or
![]() (mod 8) there is an integer
a
such that
(mod 8) there is an integer
a
such that
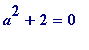 (mod
p
), and that can't be proved using Wilson's theorem...
(mod
p
), and that can't be proved using Wilson's theorem...
One may also prove this theorem:
Theorem
. Let
p
be any prime with
![]() (mod 6) then
(mod 6) then
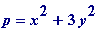 for some integers
x
and
y
.
for some integers
x
and
y
.
Examples
.
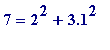 ,
,
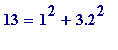 ,
,
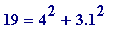 ,
,
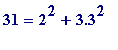 , ...
, ...
Really, really interesting things start at
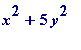 ... (Ah, if only one had time...)
... (Ah, if only one had time...)
And much, much more is known about the two squares in
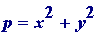 .
.
To start with it can be proved that the pair (
![]() ) is
unique
(apart from interchange, or change of sign).
) is
unique
(apart from interchange, or change of sign).
Also, there are four quite beautiful structured ways for finding x and y :
-
Legendre (1808). Here one needs to know about the (infinite, but periodic) continued fraction expansion of
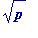
-
Gauss (1825). His construction is simple, but hard to
prove
: let
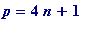 and set:
and set:
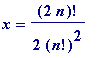 (mod
p
)
and
(mod
p
)
and
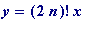 (mod
p
) with
(mod
p
) with
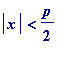 and
and
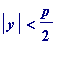 , then
, then
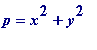
-
Serret (1848). Here one needs to know about (finite) continued fraction expansions of rational numbers, and here the relevant rational is
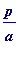 , where
, where
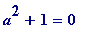 (mod
p
) with positive
a
less than
(mod
p
) with positive
a
less than
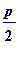 .
.
-
Jacobsthal (1906). Here one needs to know about quadratic residues, and Jacobsthal's beautiful result involves a careful study of sums of Legendre symbols,
![S[r] = Sum([n*(n^2-r)/p],n = 0 .. p-1)](images/Fermat-Thue 2-squares259.gif) (here I have been forced to use square brackets for the Legendre symbol) for non-zero residues
r
. Remarkably it emerges that
(here I have been forced to use square brackets for the Legendre symbol) for non-zero residues
r
. Remarkably it emerges that
![S[r]](images/Fermat-Thue 2-squares260.gif) has only
two
values, and you've probably guessed what those are!!
has only
two
values, and you've probably guessed what those are!!
An outstanding reference is Harold Davenport's The Higher Arithmetic (I had the great good fortune (in Feb 1995) to come upon a 1952 first edition - in a run-down bookshop near where I live - for �3!!), though there are more recent editions.