The Erdös-Strauss conjecture

Introduction. The greedy-algorithm result tells one that

• where is a fraction whose numerator is less than a .
• where is a fraction whose numerator is less than
• where is a fraction whose numerator is less than
  
  etc

The sequence is strictly monotonic decreasing, which eventually terminates when one has , for some r . For a given a , there will then be at most a terms in the sequence of unit fractions: , and clearly the maximum can happen in the event that the sequence happens to be the natural numbers less than a : .

Thus, using the greedy algorithm :

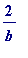• will require at most 2 unit fractions
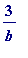• will require at most 3 unit fractions
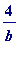• will require at most 4 unit fractions
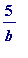• will require at most 5 unit fractions
  
  etc

Conjecture (Erdös-Strauss). For every natural number n , greater than 3, there is an Egyptian fraction representation that is better than the one ensured by the greedy algorithm representation; in other words: for every integer n (greater than 3) there are natural numbers x , y and z such that

Interested readers may consult Chapter 30 of Mordell's Diophantine Equations .

Some elementary ideas (which could be at school level). Using

Thus, setting n = 3 x + 2 ( x = 0, 1, 2, 3, 4, 5, ... ), we have that the Erdös-Strauss conjecture is (trivially) true for all such n .