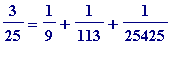Fibonacci's greedy algorithm
What I write here is meant only to be a summary after the event , after the playing/experimentimg/teaching has been done in some way...
Let's start with a (well-chosen!) example like '
'. Let's try to fill in the question marks on the right-hand side of:
= ? + ? + ... + ? [e]
with
distinct unit fractions
. What unit fractions might one try? An
obvious
initial observation is that one could
not use
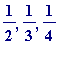, ... (Why? Because they are
too big
in relation to
). And
where
does the '...' end? Of course it ends at
because
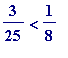(which is
), while
.
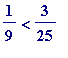So, [e] could
-
not
commence with
+ ? + ... + ?,
-
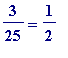nor
with
+ ? + ... + ?,
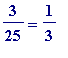- nor with ...
-
nor
with
+ ? + ... + ?,
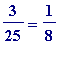but
-
it
could
commence with
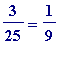+ ? + ... + ? [e9], and
-
it
could also
commence with
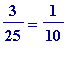+ ? + ... + ? [e10], and
-
it
could also
commence with
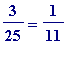+ ? + ... + ? [e11]
etc
,
etc
So much choice ! An infinite amount of choice, in fact... which is what makes it all so interesting...
Suppose one made the choice in [e9]; then one would
do the obvious thing
: subtract
from the right-hand side of [e9] giving
=
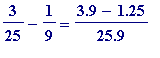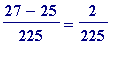= ? + ... ? [e9', is unfinished]
But if one made the choice in [e10] then one would have
=
=
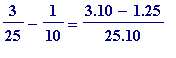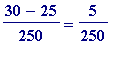[e10', is finished]
Thus
.
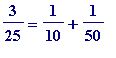If one were to continue with the '
' in [e9'] by setting
= ? + ... + ? [e9'']
then the
first possible unit fraction
(as we did earlier to produce the initial '
'; this is an
important detail
which I will return to in a moment) that one could use is
, giving:
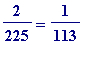+ ... + ? [e9''']
Thus
=
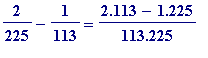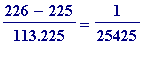, and so the initial choice of
has led to
