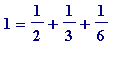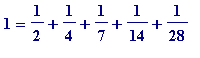Problems

Problem(s) 1. An integer can be the sum of reciprocals of distinct integers (do you see how these ones come from perfect numbers?):

  • 1 = 1/2+1/3+1/6
  • 1 = 1/2+1/4+1/7+1/14+1/28

Can you make up some more? And how about triply-perfect numbers producing:

2 = 1/n[1]+1/n[2]+1/n[3]+`...` , with distinct unit fractions 1/n[1], 1/n[2], 1/n[3], `...`

Write a program that would enable you to find some triply-perfect, quadruply-perfect numbers, etc (with a view to finding sums of distinct unit fractions that add up to (1), (2), 3, 4, 5, ... )

Problem 2. Prove that no integer can be expressed as a sum of reciprocals of distinct primes .

Problem 3. Prove 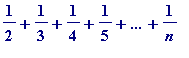1/2+1/3+1/4+1/5+`...`+1/n is never an integer.

Contact details 

After August 31st 2007 please use the following Gmail address: jbcosgrave at gmail.com

This page was last updated 18 February 2005 15:07:04 -0000