> # visible structures.mws
> restart;
> with(plots): # this is needed later for 'display'
Warning, the name changecoords has been redefined
>
Seeing
(of a
sort
)
is believing
(up to a
point
)
...
John Cosgrave, Mathematics Department,
St. Patrick's College, Drumcondra, Dublin 9,
IRELAND
[email protected]
Acknowledgement . The inspiration for this Maple worksheet was an article (rather one particular diagram in an article: Figure 1 on page 899) - Visible Structures in Number Theory - by Peter Borwein and Loki J�rgenson in the December 2001 issue of the American Mathematical Monthly ; their diagram illustrates that the sum of the Archimedean series (as I refer to it)
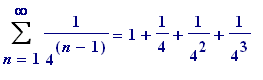 + ...
ad infinitum
+ ...
ad infinitum
is
![]() .
.
Preamble . Forget about the technology (for the moment); just use your imagination ... Here's something I first read somewhere when I was at school; it relates to the sum of the infinite series:
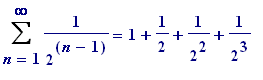 + ...
ad infinitum
+ ...
ad infinitum
whose sum is 2.
Here's how one may see the (essential) truth of that:
take in hand (imagine having) a piece of string, L , of length 2, and
-
cut that string into two pieces,
![L[1]](images/visible structures4.gif) and
and
![E[1]](images/visible structures5.gif) , of equal length; then one has:
, of equal length; then one has:
![]() (hardly a surprise!)
(hardly a surprise!)
-
cut that string
![E[1]](images/visible structures7.gif) into two pieces,
into two pieces,
![L[2]](images/visible structures8.gif) and
and
![E[2]](images/visible structures9.gif) , of equal length (
, of equal length (
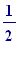 ); then one has:
); then one has:
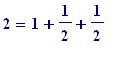
-
cut that string
![E[2]](images/visible structures12.gif) into two pieces,
into two pieces,
![L[3]](images/visible structures13.gif) and
and
![E[3]](images/visible structures14.gif) , of equal length (
, of equal length (
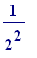 ); then one has:
); then one has:
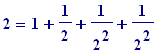
-
cut that string
![E[3]](images/visible structures17.gif) into two pieces,
into two pieces,
![L[4]](images/visible structures18.gif) and
and
![E[4]](images/visible structures19.gif) , of equal length (
, of equal length (
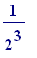 ); then one has:
); then one has:
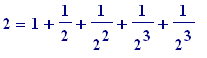
..............................
-
cut that string
![E[n]](images/visible structures22.gif) into two pieces,
into two pieces,
![L[n+1]](images/visible structures23.gif) and
and
![E[n+1]](images/visible structures24.gif) , of equal length (
, of equal length (
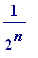 ); then one has:
); then one has:
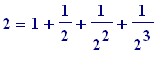 + ... +
+ ... +
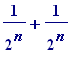
The crux
. Now
imagine
the original string cut into an
infinite
number of pieces:
- one piece having length 1
-
a
 piece having length
piece having length
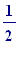
-
a
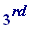 piece having length
piece having length
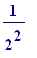
-
a
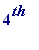 piece having length
piece having length
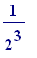
-
a
 piece having length
piece having length
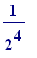
... and so on ad infinitum
Then (stating the intuitive:) the length of the original string is equal to the total sum of the individual pieces of string, we would see that:
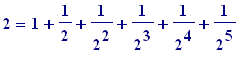 + ...
ad infinitum
+ ...
ad infinitum
Moving on . Elsewhere I have explained that the first genuine example of what is now called an infinite series could be said to have occurred implicitly in the work of Archimedes (though that is bending the true history... , as mathematical historians will know; however I never let historical accuracy get in the way of the more important issue: understanding mathematical ideas )
I have attempted elsewhere to convey to you (my students), that one of the initial hurdles to be overcome in connection with understanding infinite series is that of realising that it is a non-trivial problem to define exactly what is meant by the sum of such a series... .
Recall that naively one might think every series (within reason, of course) actually has a sum, and one might also think that the only problem is to find - by some clever method ( Let S be the sum of the series, then multiplying S by ... , and then subtracting, and then ... , and so the actual value of S is ... ) or whatever - the value of that sum...
The aim of this worksheet is to show some pictures which attempt to reinforce an understanding of the sums of certain infinite series. I will begin by setting up some pictures which allow one to see (but your imagination will play a very big role in all this!) that the series encountered in the Archimedes work:
 + ... +
+ ... +
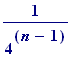 + ...
ad infinitum
, has sum
+ ...
ad infinitum
, has sum
![]() .
.
This is what I am going to do:
-
First I am going to show you
a
picture, in which you will see some squares fitting together in a certain (
clever
) way; it is the
initial
part of a picture that
no
computer could construct, because the picture that I want you to
see
can only be
seen
in your
imagination
... (later I will show you an animation whose final frame is this single, static picture...)
Figure 1 in the Borwein-J�rgenson December 2001 Monthly article
![[Maple Plot]](images/visible structures40.gif)
-
Next I give some
details
about those squares:
0. The largest, outer square has side length 2,
and as for the green squares, starting at the bottom left-hand corner:
1. the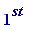 of them has side
length
1, and so has area...
of them has side
length
1, and so has area...
2. the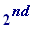 of them has side
length
of them has side
length
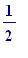 (simply
(simply
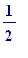 the length of the
the length of the
 square)
square)
3. the of them has side
length
of them has side
length
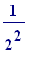 (simply
(simply
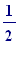 the length of the
the length of the
 square)
square)
4. the of them has side
length
of them has side
length
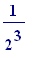 (simply
(simply
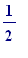 the length of the
the length of the
 square)
square)
... ... ... ... ...
k . the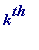 of them has side
length
of them has side
length
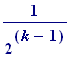 (simply
(simply
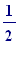 the length of the
the length of the
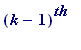 square)
square)
-
Lastly, I ask you this question:
How
does the
imagined diagram
support the claim that the
sum
of the
infinite
series
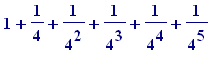 + ... +
+ ... +
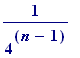 + ...
ad infinitum
is
+ ...
ad infinitum
is
![]() ?
?
Comment . Notice, by the way, that the side length - 2 - of the above square is the sum of the infinite series:
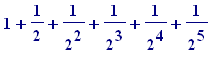 + ...
+ ...
In the following Maple program, I am simply forming the first 7 partial sums
![]() , ... ,
, ... ,
![]() of the infinite series:
of the infinite series:
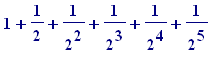 + ... +
+ ... +
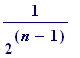 + ...
ad infinitum
+ ...
ad infinitum
they are given by:
![]()
![s[1]+s[2] = 1+1/2](images/visible structures67.gif)
![s[1]+s[2]+s[3] = 1+1/2+1/(2^2)](images/visible structures68.gif)
![s[1]+s[2]+s[3]+s[4] = 1+1/2+1/(2^2)+1/(2^3)](images/visible structures69.gif) , etc
, etc
In short, we have:
![]() ,
,
![s[k] = s[k-1]+1/(2^(k-1))](images/visible structures71.gif) for
for
![]() .
.
>
n := 7: s[1] := 1:
for k from 2 to n do
s[k] := s[k-1] + 1/2^(k-1) od:
seq(s[k], k = 1..n);
![]()
>
s[0] := 0: for r to n do
square||r := PLOT(seq(POLYGONS([[s[k-1],s[k-1]], [s[k],s[k-1]],[s[k],s[k]], [s[k-1],s[k]]], COLOUR(RGB,0,1,0)), k=1..r)):
above||r := PLOT(seq(POLYGONS([[s[k-1],s[k]], [s[k],s[k]],[s[k],2], [s[k-1],2]], COLOUR(RGB,0,0,1)), k=1..r)):
below||r := PLOT(seq(POLYGONS([[s[k],s[k-1]], [2,s[k-1]],[2,s[k]], [s[k],s[k]]], COLOUR(RGB,0,0,1)), k=1..r)):
outer_square := PLOT(POLYGONS([[0,0],[2,0],[2,2], [0,2]], COLOUR(RGB,1,1,1))):
show||r := display([square||r, above||r,
below||r, outer_square]):
od: display([show||(1..n)], insequence=true);
![[Maple Plot]](images/visible structures74.gif)
> # display([show||n]); # to make the initial picture
>
Comment . Motivated by the above (which requires an in-class discussion) there are many directions in which one might go, but one obvious one is to ask: what other infinite series might have their sums illustrated by varying the above diagram: for example by dividing a square into a 3 by 3 (or 4 by 4, etc) grid...
The following (which requires some discussion is an initial step down that road)...
>
n := 10: s[1] := 1:
for k from 2 to n do
s[k] := s[k-1] + (2/3)^(k-1) od:
seq(s[k], k = 1..n);
![]()
>
s[0] := 0: for r to n do
square||r := PLOT(seq(POLYGONS([[s[k-1],s[k-1]], [s[k],s[k-1]],[s[k],s[k]], [s[k-1],s[k]]], COLOUR(RGB,0,1,0)), k=1..r)):
above||r := PLOT(seq(POLYGONS([[s[k-1],s[k]], [s[k],s[k]],[s[k],3], [s[k-1],3]], COLOUR(RGB,0,0,1)), k=1..r)):
below||r := PLOT(seq(POLYGONS([[s[k],s[k-1]], [3,s[k-1]],[3,s[k]], [s[k],s[k]]], COLOUR(RGB,0,0,1)), k=1..r)):
outer_square := PLOT(POLYGONS([[0,0],[3,0],[3,3], [0,3]], COLOUR(RGB,1,1,1))):
show||r := display([square||r, above||r,
below||r, outer_square]):
od: display([show||(1..n)], insequence=true);
![[Maple Plot]](images/visible structures76.gif)
>
>
n := 14: s[1] := 1:
for k from 2 to n do
s[k] := s[k-1] + (3/4)^(k-1) od:
seq(s[k], k = 1..n);
![]()
>
s[0] := 0: for r to n do
square||r := PLOT(seq(POLYGONS([[s[k-1],s[k-1]], [s[k],s[k-1]],[s[k],s[k]], [s[k-1],s[k]]], COLOUR(RGB,0,1,0)), k=1..r)):
above||r := PLOT(seq(POLYGONS([[s[k-1],s[k]], [s[k],s[k]],[s[k],4], [s[k-1],4]], COLOUR(RGB,0,0,1)), k=1..r)):
below||r := PLOT(seq(POLYGONS([[s[k],s[k-1]], [4,s[k-1]],[4,s[k]], [s[k],s[k]]], COLOUR(RGB,0,0,1)), k=1..r)):
outer_square := PLOT(POLYGONS([[0,0],[4,0],[4,4], [0,4]], COLOUR(RGB,1,1,1))):
show||r := display([square||r, above||r,
below||r, outer_square]):
od: display([show||(1..n)], insequence=true);
![[Maple Plot]](images/visible structures78.gif)
>