> # Swineshead.mws
> restart;
>
A Maple worksheet devoted to Swineshead's series (as I call it)
John Cosgrave, St. Patrick's College, Drumcondra,
Dublin 9, IRELAND.
[email protected]
Swineshead's series (from C.H.Edwards' The Historical Development of the Calculus : 'Richard Swineshead (known to medievals as the Calculator, as Aristotle was the Philosopher and Paul the Apostle) was part of a group working in Merton College (Oxford) during the second quarter of the 1300's).
Swineshead found the sum of the following series (pay special attention to its
formation
), it is
- partly 'arithmetic' progression: the 1, 2, 3, 4, ... , n , ...
-
partly 'geometric' progression: the
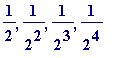 , ... ,
, ... ,
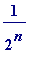 , ...
, ...
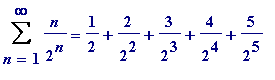 + ...
ad infinitum
+ ...
ad infinitum
to be 2
.
Before going any further, you should mentally
consider
(think about!) the first few partial sums:
![s[1] = 1/2](images/Swineshead's sum4.gif)
![s[2] = 1/2+2/(2^2)](images/Swineshead's sum5.gif) =
=
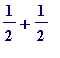 ( = 1 )
( = 1 )
![s[3] = 1/2+2/(2^2)+3/(2^3)](images/Swineshead's sum7.gif) =
=
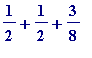 ( =
( =
![]() )
)
![s[4] = 1/2+2/(2^2)+3/(2^3)+4/(2^4)](images/Swineshead's sum10.gif) =
=
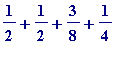 ( =
( =
![]() )
)
![s[5] = 1/2+2/(2^2)+3/(2^3)+4/(2^4)+5/(2^5)](images/Swineshead's sum13.gif) =
=
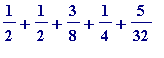 ( =
( =
![]() )
)
![s[6] = 1/2+2/(2^2)+3/(2^3)+4/(2^4)+5/(2^5)+6/(2^6)](images/Swineshead's sum16.gif) =
=
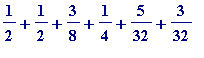 ( =
( =
![]() =
=
![]() )
)
... ... ...
Question . Can you write a Maple program to produce those partial sums? How about the first 50 of them? At this point I ask you to tell me... (and in this worksheet I place it at the end...).
>
>
[Aside: It is not at all obvious what the
infinite
sum is!!] Swineshead found the
sum
to be 2, but by a method (
entirely verbal
) that would not be acceptable today. I will show you how that '2' may be arrived at, again by a method not
strictly
acceptable; the method is entirely familiar, and is the one already known from school for finding the sum of a
geometric series
(which the above series is
not
), and has already been encountered by you in the purely formal of the sum of the Archimedes series (
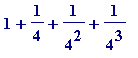 + ...
ad infinitum
). With the Archimedes series the trick was to multiply by
+ ...
ad infinitum
). With the Archimedes series the trick was to multiply by
![]() ; here it is to multiply by
; here it is to multiply by
![]() :
:
Let
S
= (
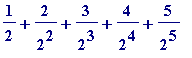 + ...
ad infinitum
)
...
( i )
+ ...
ad infinitum
)
...
( i )
then
![]()
![]() =
=
![]() (
(
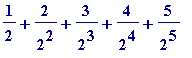 + ...
ad infinitum
)
+ ...
ad infinitum
)
=
(
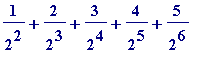 + ...
ad infinitum
) ... ( ii )
+ ...
ad infinitum
) ... ( ii )
Formal subtraction of ( ii ) from ( i ) gives
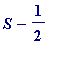 S
= (
S
= (
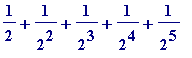 + ...
ad infinitum
)
+ ...
ad infinitum
)
(and the right hand side has
known
sum
'1')
giving (
apparently
)
![]()
![]() , and (
so
)
, and (
so
)
![]() .
.
________________________
A second (non-rigourous!) way in which one may formally uncover that the sum is 2:
Start as we did above:
Let
S
= (
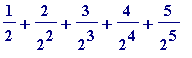 + ... ), and then continue:
+ ... ), and then continue:
so,
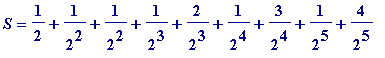 + ...
+ ...
= (
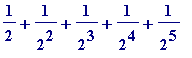 + ... ) + (
+ ... ) + (
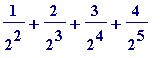 + ... )
+ ... )
= ( 1 ) +
![]() *(
*(
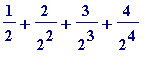 + ... )
+ ... )
namely:
![]() +
+
![]() *
S
, giving
*
S
, giving
![]() .
.
Comment
. In fact it is preferable to view that in general terms (without the
distraction
of the '
![]() '):
'):
Let
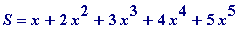 + ...
ad infinitum
)
...
( i )
+ ...
ad infinitum
)
...
( i )
then
![]()
![]() =
=
![]() (
(
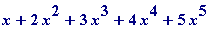 + ...
ad infinitum
)
+ ...
ad infinitum
)
=
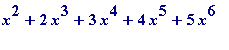 + ...
ad infinitum
... ( ii )
+ ...
ad infinitum
... ( ii )
Formal subtraction of ( ii ) from ( i ) gives
![]() S
=
S
=
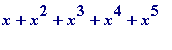 + ...
ad infinitum
+ ...
ad infinitum
(and the right hand side has
known
sum
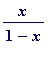 ,
provided
x
lies
between
-1 and 1)
,
provided
x
lies
between
-1 and 1)
giving (
actually
) that
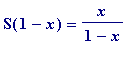 , and so
, and so
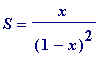 provided
provided
![]() < 1.
< 1.
__________________________
According to Edwards' History , page 88: 'The Merton studies spread to France and Italy in the mid-fourteenth century. In his Treatise on the Configurations of Qualities and Motions , written in the 1350s, the Parisian scholastic Nicole Oresme introduced the important concept of graphical representations [my emphasis, JC] ...
and, page 92: 'In his Treatise , Oresme gave a geometric method for summing [the above Swineshead series]...'. This worksheet demonstrates the Oresme method.
>
n := 7: s[1] := 1/2:
for k from 2 to n do
s[k] := s[k-1] + 1/2^k od:
seq(s[k], k = 1..n);
![]()
> with(plots): # needed for 'display' in the following
Warning, the name changecoords has been redefined
>
Note
. One should
reduce
the frame speed to 1 in the animations...
One should
notice
in the following diagrams that:
-
the areas of the
green
rectangles (the A's) are given by:
1. 1 (height) *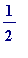 (base length)
(base length)
and that the area of the white rectangle to its right is...
2. 2 (height) *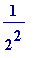 (base length)
(base length)
and that the area of the white rectangle to its right is...
3. 3 (height) *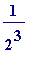 (base length)
(base length)
and that the area of the white rectangle to its right is...
4. 4 (height) *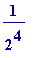 (base length)
(base length)
and that the area of the white rectangle to its right is...
and that the suggested total area of the infinitely many green rectangles is ...
.................. -
the areas of the
blue
rectangles (the B's) are given by:
1. 1 (height) * 1 (base length)
2. 1 (height) *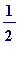 (base length)
(base length)
3. 1 (height) *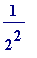 (base length)
(base length)
4. 1 (height) *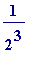 (base length)
(base length)
... ...
The sum of the areas of all the infinitely many blue rectangles is...
Thus one sees that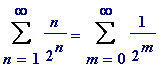 = 2.
= 2.
>
s[0] := 0: for r to n do
A||r := PLOT(POLYGONS([[s[r-1],0],[s[r],0],[s[r],r],
[s[r-1],r]],COLOUR(RGB,0,1,0))):
B||r := PLOT(POLYGONS([[s[r-1],r-1],[1,r-1],[1,r],
[s[r-1],r]],COLOUR(RGB,0,0,1))):
a||r := PLOT(POLYGONS([[s[r],0],[1,0],[1,r],
[s[r],r]],COLOUR(RGB,1,1,1)))
od:
for r to n do
all_A||r := display(A||(1..r)):
all_B||r := display(B||(1..r)):
G||r := array(1..2):
G||r[1] := display([all_A||r, a||r]):
G||r[2] := all_B||r:
show||r := display(G||r):
od:
display([show||(1..n)], insequence=true);
![[Maple Plot]](images/Swineshead's sum65.gif)
>
A simple Maple program to find the first 40 partial sums of the Swineshead series:
>
s[1] := 1/2^1;
for k from 2 to 40 do
s[k] := s[k-1] + k/2^k
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>
for k to 40 do
[k, evalf(s[k])]
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>
There - using 'evalf' - the decimal computations are automatically done to 10 places, but one can do them to 50 places (for example), and for the first 120 of the partial sums, by doing this:
>
s[1] := 1/2^1:
for k from 2 to 120 do
s[k] := s[k-1] + k/2^k
od:
for k to 120 do
[k, evalf(s[k], 50)]
od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>